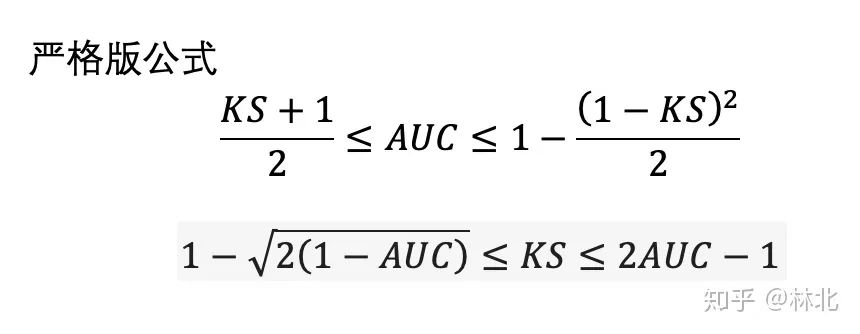在业务中,很多人使用AUC/KS时仅关注数值大小,却无视样本逾期率和样本量等要素,这是个严重问题。像AUC/KS常用来评估二分类模型等的区分度,仅看数值并不足以准确判断模型或数据产品的真实好坏程度。
AUC/KS评估的常见认知
AUC/KS是评估二分类模型、分数类数据产品区分度的常用指标。很多人认为,只要AUC/KS值高,模型就是好模型。例如在某些小型金融科技公司研发信用评分模型时,仅仅依据AUC/KS数值就判断模型优劣。但实际上,这还不够全面。它只是从一个角度进行评估,并没有涵盖全部重要信息。现实场景中的评估需要考虑更多因素,而非单纯一个数值的表象。
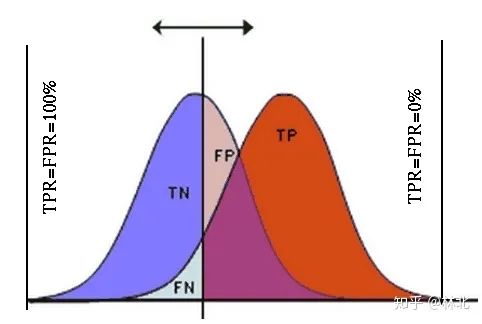
其实AUC和KS分别从不同角度刻画好坏样本信用分数的分布距离。但人们往往过于依赖数值带来的直观感受,而不深入探究背后样本的真实情况。比如在一些业务竞赛中,选手们只追求AUC/KS的高数值,忽略了其他可能影响结果的因素。这不利于对模型或产品做出准确和全面的评估。
测试样本逾期率的影响
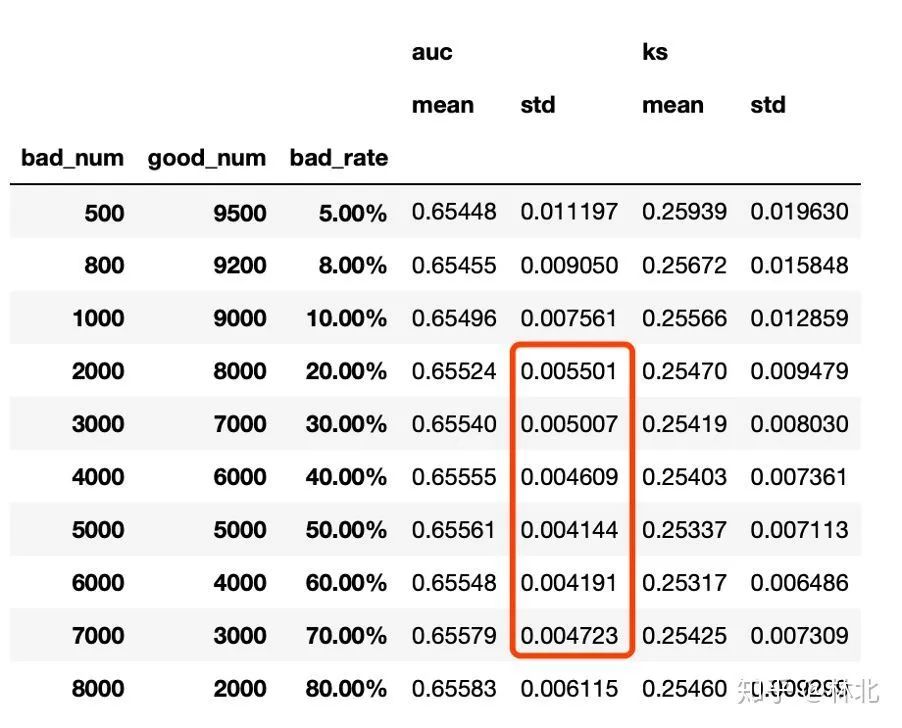
测试样本逾期率对于AUC/KS的计算具有微妙关系。通常来说,测试样本逾期率在10%到20%较为合适。像以前有公司使用50%逾期率的样本进行数据测试,这是很不科学的做法。在这里,逾期率过高或者过低都不合适。在实际操作中,如果忽略缺失和抽样误差,仅仅从计算公式上讲,不同逾期率的测试样本在计算AUC/KS时,其值在理论上应该是一致的。
为了验证,我们进行了模拟。我们对每种逾期率下重复100次计算。结果是,不同逾期率的测试样本下计算的AUC/KS均值基本一致,只是标准差有所差异。这就表明,在考虑是否会影响AUC/KS的问题上,逾期率不像大多数人认为的有那么大影响。它更多地是在影响计算结果的稳定性,而非本质上改变AUC/KS的数值。
抽样误差与样本量的关系
样本量的大小和抽样误差紧密相连。当样本量过小的时候,会导致抽样误差过大,进而影响AUC/KS的计算。实际经验表明,只要好坏样本的绝对数量都大于1000,抽样误差对AUC/KS的影响就很小。比如说在一个有5000个样本的测试中,其中好坏样本都超过1000个时,抽样误差就基本可以忽略不计了。
在评估的实际流程中,我们为了减小与刻画抽样误差,会进行多次抽样。在调整测试样本量的同时,针对同一款信用分计算AUC/KS的大小。多样本量下都重复100次计算平均的AUC/KS以及对应的标准差。在这个过程中可以明显看到不同样本量对整体结果的影响以及如何控制抽样误差的影响。
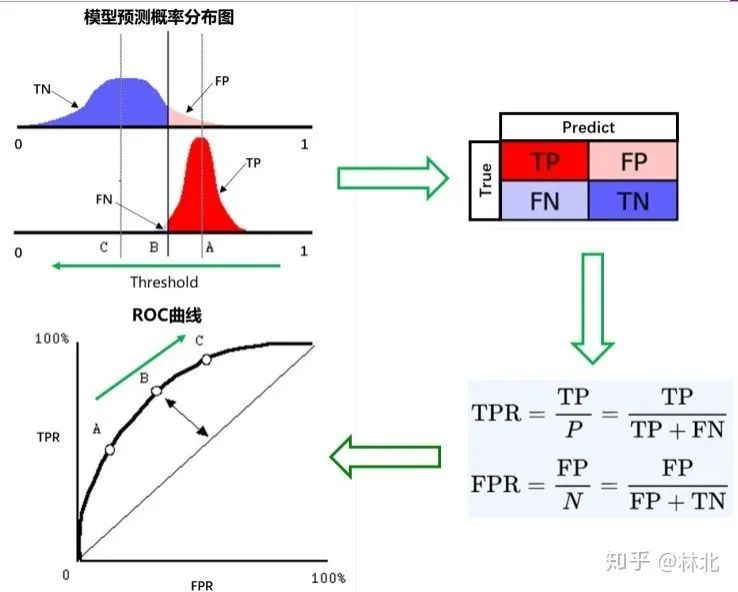
回顾AUC/KS的定义
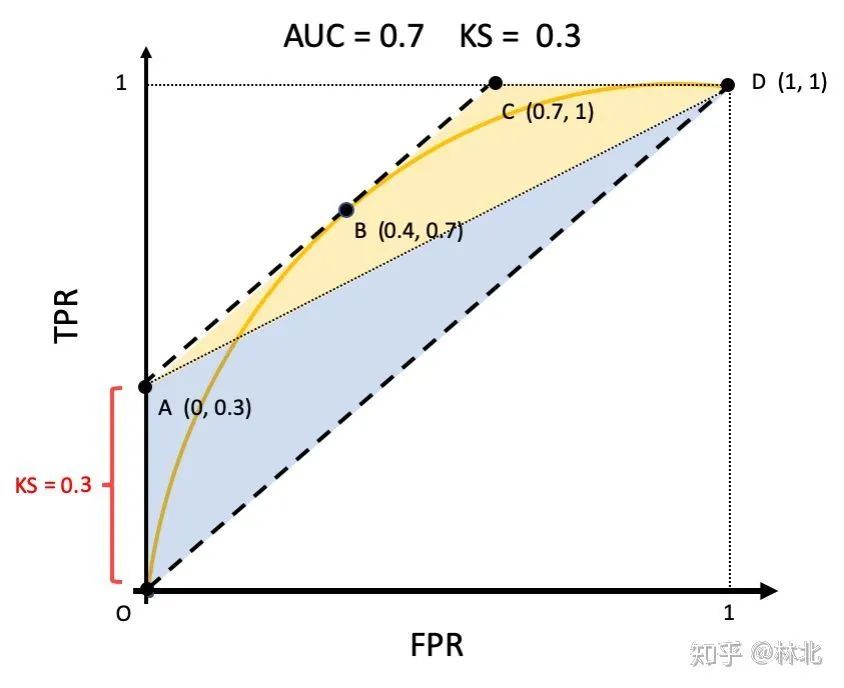
回顾AUC/KS的定义能够帮助我们更好地理解这些指标。AUC/KS都是基于TPR、FPR得到的。因为TPR与FPR不会被好坏样本的相对数量所影响。这也就导致了在不同逾期率的测试样本,在同一个划分节点下,虽然TP、FP、FN、TN的绝对数量会发生变化,但TPR与FPR是一致的,进而AUC/KS也是一致的。
比如在一个已经内部验证过的小型信用评估模型的数据验证中,无论改变样本逾期率还是样本量在一定范围内,AUC/KS的一致性都体现了这种基于定义的不变性。这也告诉我们在解读AUC/KS时需要依据定义的本质来考量,不要被一些表面现象所迷惑。
好坏样本分布的一致性
在整个AUC/KS的评估过程中,真正对其产生关键影响的是测试样本中好坏样本的分布与总体分布的一致程度。如果说逾期率和样本量是较大框架下容易被关注到的因素,那么好坏样本分布的一致性则是更加隐藏在背后的因素。例如在一个评估贷款违约情况的模型里,如果测试样本中好坏样本的分布与总体分布差异过大,那么计算出来的AUC/KS数值即便看上去不错,也要持谨慎态度。
有种情况是,在不注意好坏样本分布一致性的情况下,误判模型的好坏。因为一个模型可能在与总体分布一致的样本中有很好的表现,但当样本分布与总体不同时,它的AUC/KS数值可能会产生误导性的结果。
AUC/KS使用的总结与启示
在使用AUC/KS的时候,不能只看数值大小,要综合考虑样本逾期率、样本量以及好坏样本分布的一致性等多个因素。只有这样,才能对二分类模型、分数类数据产品做出准确合理的评估。许多业务人员和建模专家忽视这些要素而只关注数值,是导致评估不准确的重要原因。在实际业务场景中,我们应该如何更有效地提高模型评估的准确性,避免陷入这种只看AUC/KS数值的陷阱?希望大家能在评论区分享自己的看法,也欢迎大家点赞和分享本文。